昨日、「人間は考える管」で、管は身体の中にあるけれど外と同じという訳のわからない話をしました。トポロジーに出てくる不思議な立体に「クラインの壺」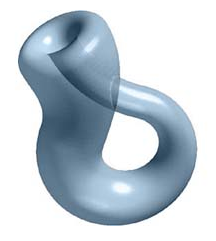
（引用：http://earth2010.exblog.jp/10991635/）があります。壺の中に入って行くといつの間にか壺の表面に出てしまうというものです。人間の中の管に似ていますね。 次に、これも皆さんがご存知のメビウスの輪です。これもトポロジーでよく出てくる例です。輪の表を歩いていくと、いつの間にか裏に行ってしまうのです。そして、ハサミで真中を切っていくと２つのリングではなく、元の倍の大きさのリングになりますね。このメビウスの輪もいろいろな変形バージョンがあって、手品や余興にも使えますよ。では問題を３つ出します。問題１は、二つのメビウスの輪を十字に貼り付けて２つの輪の中央をハサミで切断しますが、A：２つのメビウスの輪はねじる方向を反対にする場合とB:同じ方向にねじる場合があります。どちらか好きな方を選んで切断してみてください。「恋占いです」さあ、どちらがハッピーになるか？ 良い結果にならなくても気にしないでください。当たるかどうかは保証しませんので。 問題２は、メビウスの輪にしない（ねじらない）で十字に貼り付けます。問題１と同様に２つの輪の中央をハサミで切断します。さて、どんな形状になるでしょうか？想像してみてください。今度は２つに分かれますか？ 問題３は、メビウスの輪の３分の１のところをハサミで切断していきます。 さて、これはどうでしょうか？
クリックしてください→ メビウスの輪
クリックしてください→ メビウスの輪解答
いかがでしたか？ まずは頭で考えて予想してから、実際に作製して切断してみてください。メビウスの輪はこの他にもいろいろなパターンがあります。下記の資料をご覧ください。
クリックしてください→ メビウスの輪で遊ぼう（野呂茂樹 著）
英語も一緒に勉強したい方は、以下のYouTubeをご覧ください。開始１１分頃から問題３の実演が見られます。ケンブリッジ大の時枝正先生の講義です。日本人なので、英語は聴き易いですよ。
クリックしてください→ Topology & Geometry - LECTURE 01 Part 01/02 - by Dr Tadashi Tokieda